Con esta entrada se pretende dar una explicación básica a la necesidad del estudio de la topografía en el modulo de Grado Medio de Trabajos Forestales y Conservación del Medio Natural, es lo básico que se debe aprender y si es posible más para poder desarrollar vuestro futuro trabajo correctamente.
Para ello voy a exponer un problema tipo que sería interesante que todos los alumnos pudieran desarrollar.
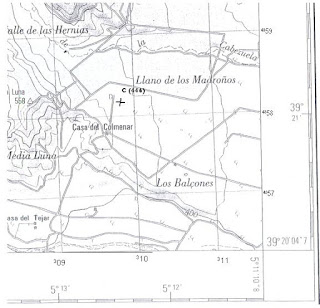
Teniendo el siguiente plano:
2. Determina en el plano el punto A; sabiendo que las coordenadas geográficas son (39º 21´14” N, 5º11´43” O)
3. Determina en el plano el punto B; sabiendo que las coordenadas UTM son (311120, 4357480)
4. Determina las coordenadas UTM del punto C del plano de arriba.
5. Determina la superficie generada por los 3 puntos anteriores, teniendo en cuenta la escala determinada en el punto 1 y utilizando la fórmula de Herón.
6. Determina la distancia reducida entre el punto C y la cumbre denominada Luna.
7. Determina el desnivel existente entre los puntos anteriores.
8. Determina la distancia geográfica entre los puntos del apartado anterior.
9. Determina la pendiente entre el punto c y la cumbre denominada Luna y exprésalo en grados sexagesimales completos
Bien vamos a empezar!!!!!!
1. Calcula la escala del plano.
Podemos definir la escala como la relación que existe entre una distancia real y su correspondiente en la carta o mapa.
Sabemos que hay 2 tipos de escala; la numérica y la gráfica. La que nos pide en el problema es la escala numérica. Para ello, tenemos que saber que cada cuadrado que vemos en el plano es de 1Km2, esto es cada lado es mide 1 km.
Así tenemos que:
5 cm equivale a 1km
Pasándolo todo a las mismas unidades esto es a cm, no que da que:
5 cm equivale a 100000 cm.
Para hallar la escala tenemos que suponerlo a 1 cm en el plano, así nos queda el siguiente sistema:
5 cm 100000 cm
1 cm X
Despejando X, nos queda que X vale 20000
Por lo que la escala es 1:20000
2. Determina en el plano el punto A; sabiendo que las coordenadas geográficas son (39º 21´14” N, 5º11´43” O)
Nos fijamos en la escala blanca y negra de los laterales.
Todos los planos topopgráficos están orientados al norte, así el primer termino de la coordenada nos tenemos que fijar en la barra vertical, y buscamos el 39º 21´.
Tenemos que definir donde está el punto 14”, sabiendo que cada franja blanca y negra mide 10” ,el 14” se situará entre el 10” y 20”, para ajustarlo debemos tener presente la siguiente relación; si en 1,5 cm hay 10” cuantos cm seran 4”. Quedaría así:
1,5 cm 10”
X cm 4”.
Haciendo la regla de 3, sacamos que X es igual a 0,6 cm, se mide y obtenemos una linea donde va a estar situado el punto A.
Para determinar la segunda parte de la coordenada, nos fijamos en la barra horizontal, y buscamos los 5º 11´.
Como no llega hasta el 5º 11´00” , lo hacemos empezando por 5º12´y vamos hacia atrás 5º11´50”, 5º11´40”, 5º11´30”, así hasta 5º11´10”.
Los segundos que tenemos está entre 5º11´50” y 5º11´40”, ya que buscamos el 43”, tenemos que colocar el 3” . como sabemos que cada porción de 10” mide 1,5 cm; podemos proponer la siguente relación:
1,5 cm 10”
X cm 3”.
Haciendo regla de 3, sacamos que X es igual a 0,45 cm redondeando nos queda 0,5 cm, haciendo una perpendicular se cruza con el anterior y obtenemos el punto A.
El punto A quedaría:
3. Determina en el plano el punto B; sabiendo que las coordenadas UTM son (311120, 4358480)
Lo primero que tenemos que hacer es determinar la segunda parte de la coordenada, ¡¡¡es un número muy largo!!!, pero de momento nos fijamos en las primeras 4 cifras, esto es, 4358 y lo buscamos en el plano.
 Por lo tanto, sabemos que el punto B, está en una linea que se encuentra entre el 4357 y el 4358, pero habrá que ajustarlo un poco, para ello, nos fijamos en los 3 números siguientes 480. Sabemos que entre línea y línea en la realidad mide 1000 m y en el plano mide 5 cm y haciendo una regla de 3 obtenemos la línea buscada.
Por lo tanto, sabemos que el punto B, está en una linea que se encuentra entre el 4357 y el 4358, pero habrá que ajustarlo un poco, para ello, nos fijamos en los 3 números siguientes 480. Sabemos que entre línea y línea en la realidad mide 1000 m y en el plano mide 5 cm y haciendo una regla de 3 obtenemos la línea buscada.
5 cm equivale a 1000 m
x cm equivale a 480 m
Despejando, x nos da ((480x5)/1000)=2,4 cm
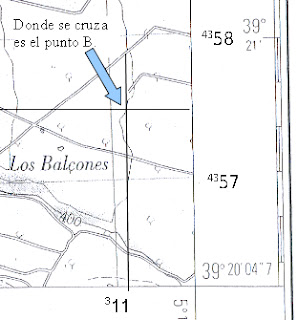
Así sabemos que el punto B se encuentra en una línea a 2,4 cm por encima de la linea 4357, como se puede ver en la imagen:
Seguimos con la primera parte de la coordenada, 311120, nos fijamos en los 3 primeros números, esto es, 311, que está localizado en el plano como se ve en la imagen.
Hay que tener en cuenta que el punto está del 311 para la derecha, ya que va a 312, aunque no se vea, se recuerda que 5 cm en el plano son 1000 m en la realidad.
Nos fijamos en los 3 puntos siguientes, esto es, 120, sabiendo la relacion anterior nos queda la siguiente regla de 3.
5 cm equivale a 1000 m
x cm equivale a 120 m.
Despejando x, nos da (120x5)/1000= 0,6 cm
Por lo que la recta que buscamos está a 0,6 cm a la derecha del punto 311 como se ve en la imagen.
Tenemos que puntualizar que este método está simplicado y se debe de recordar que las coordenadas geograficas y UTM no son paralelas entre si.
4. Determina las coordenadas UTM del punto C del plano de arriba.
Trazamos perpendiculares y paralelas a los laterales del plano desde el punto C.
Medimos lo que la distancia que hay entre 4358 y donde se cruza la línea, esto es, 0,8 cm.Sabemos que 1000 metros en la realidad son 5 cm en el plano, hacemos una regla de 3.
5 cm equivale 1000 m
0,8 cm equivale X
sacando que x vale 160 m
Por abajo medimos lo que hay entre el 309 y donde se cruza la línea, esto es, 4 cm. Haciendo lo mismo que antes, sacamos que x=800
Por lo que las coordenadas UTM del punto C son (309800, 4358160)
5. Determina la superficie generada por los 3 puntos anteriores, teniendo en cuenta la escala determinada en el punto 1 y utilizando la fórmula de Herón.
Si unimos los tres puntos, esto es, el A, B y C, forma un triángulo.
Hacemos una tabla, como sigue:
| Distancia en el plano(cm) | Distancia en la realidad (cm) | Distancia en la realidad (m) | |
| ab | 5 | 100000 | 1000 |
| bc | 7,2 | 144000 | 1440 |
| ca | 5 | 10000 | 1000 |
La primera columna es la distancia medida en el plano, la segunda columna se obtiene al multiplicar la distancia en el plano por la escala que se ha obtenido en el punto 1 dando la distancia en la realidad medida en cm. La tercera columna es la distancia en la realidad medida en metros.
Para calcular la superficie, utilizamos la fórmula de Herón, para ello, lo primero que debemos determinar es el semiperimetro (s):
6. Determina la distancia reducida entre el punto C y la cumbre denominada Luna.
Se mide la distancia que hay entre ambos puntos.
Entre ambos puntos hay una distancia de 5,8 cm. Para determinar la distancia reducida solo hace falta multiplicar por la escala, dando un resultado de 116000 cm que pasandolo a metros nos da 1160 m.
7. Determina el desnivel existente entre los puntos anteriores.
Para determinar el desnivel entre ambos puntos debemos de fijarnos en la cota de ambos puntos y simplemente restarlas, así, nos da un resultado de 112 m de desnivel.
8. Determina la distancia geográfica entre los puntos del apartado anterior.
Para hacer bien este punto debemos apoyarnos en el siguiente esquema:
Para determinar la distancia geometrica hay que aplicar el teorema de Pitágoras.
9. Determina la pendiente entre el punto c y la cumbre denominada Luna y exprésalo en grados sexagesimales completos.
La pendiente es la relación entre la distancia reducida y el desnivel existente, así aplicando la fórmula:
Estos son angulos sexagesimales incompletos y hay que pasarlo a completo:
5º
0,5149x60=30,895 30´
0,895x60=53,7 53,7”
Así queda 5º 30´53,7”












No hay comentarios:
Publicar un comentario